Last updated: 2020-05-14

Checks: 7 0

Knit directory: drift-workflow/analysis/

This reproducible R Markdown analysis was created with workflowr (version 1.6.1). The Checks tab describes the reproducibility checks that were applied when the results were created. The Past versions tab lists the development history.

R Markdown file: up-to-date

Great! Since the R Markdown file has been committed to the Git repository, you know the exact version of the code that produced these results.

Environment: empty

Great job! The global environment was empty. Objects defined in the global environment can affect the analysis in your R Markdown file in unknown ways. For reproduciblity it’s best to always run the code in an empty environment.

Seed: set.seed(20190211)

The command set.seed(20190211) was run prior to running the code in the R Markdown file. Setting a seed ensures that any results that rely on randomness, e.g. subsampling or permutations, are reproducible.

Session information: recorded

Great job! Recording the operating system, R version, and package versions is critical for reproducibility.

Cache: none

Nice! There were no cached chunks for this analysis, so you can be confident that you successfully produced the results during this run.

File paths: relative

Great job! Using relative paths to the files within your workflowr project makes it easier to run your code on other machines.

Repository version: 7ddf69c

Great! You are using Git for version control. Tracking code development and connecting the code version to the results is critical for reproducibility.

The results in this page were generated with repository version 7ddf69c. See the Past versions tab to see a history of the changes made to the R Markdown and HTML files.

Note that you need to be careful to ensure that all relevant files for the analysis have been committed to Git prior to generating the results (you can use wflow_publish or wflow_git_commit). workflowr only checks the R Markdown file, but you know if there are other scripts or data files that it depends on. Below is the status of the Git repository when the results were generated:


Ignored files:
    Ignored:    .snakemake/
    Ignored:    data/datasets/
    Ignored:    data/raw/
    Ignored:    data/simulations/
    Ignored:    nb-log-1324132.err
    Ignored:    nb-log-1324132.out
    Ignored:    notebooks/.ipynb_checkpoints/
    Ignored:    output/
    Ignored:    sandbox/.ipynb_checkpoints/

Unstaged changes:
    Modified:   analysis/OutOfAfrica_3G09.Rmd
    Modified:   code/structure_plot.R

Note that any generated files, e.g. HTML, png, CSS, etc., are not included in this status report because it is ok for generated content to have uncommitted changes.

These are the previous versions of the repository in which changes were made to the R Markdown (analysis/AmericanAdmixture_4B11.Rmd) and HTML (docs/AmericanAdmixture_4B11.html) files. If you’ve configured a remote Git repository (see ?wflow_git_remote), click on the hyperlinks in the table below to view the files as they were in that past version.

File	Version	Author	Date	Message
Rmd	7ddf69c	Joseph Marcus	2020-05-14	wflow_publish(“AmericanAdmixture_4B11.Rmd”)
Rmd	afde105	Joseph Marcus	2020-05-13	added American admixture simulation
html	407a5b0	Joseph Marcus	2020-05-13	Build site.
Rmd	90947d3	Joseph Marcus	2020-05-13	wflow_publish(“analysis/AmericanAdmixture_4B11.Rmd”)

Here I visualize population structure with simulated data from the AmericanAdmixture_4B11 scenario. See Browning et al. 2018 for details.

Imports

Import the required libraries and scripts:

suppressMessages({
  library(lfa)
  library(flashier)
  library(drift.alpha)
  library(ggplot2)
  library(reshape2)
  library(tidyverse)
  library(RColorBrewer)
  library(alstructure)
  source("../code/structure_plot.R")
})

Data

data_path <- "../output/simulations/AmericanAdmixture_4B11/rep1.txt"
Y <- t(as.matrix(read.table(data_path, sep=" ")))
n <- nrow(Y)
maf <- colSums(Y) / (2*n)
colors <- brewer.pal(8, "Set2")

# filter out too rare and too common SNPs
Y <- Y[,((maf>=.05) & (maf <=.95))]
p <- ncol(Y)
Z <- scale(Y)
print(n)

[1] 160

print(p)

[1] 24643

# sub-population labels from stdpop
labs <- rep(c("AFR", "EUR", "ASIA", "ADMIX"), each=40)

we end up with 160 individuals and ~24643 SNPs.

PCA

Lets run PCA on the centered and scaled genotype matrix:

svd_res <- lfa:::trunc.svd(Z, 5)
L_hat <- svd_res$u
plot_loadings(L_hat, labs) + scale_color_brewer(palette="Set2")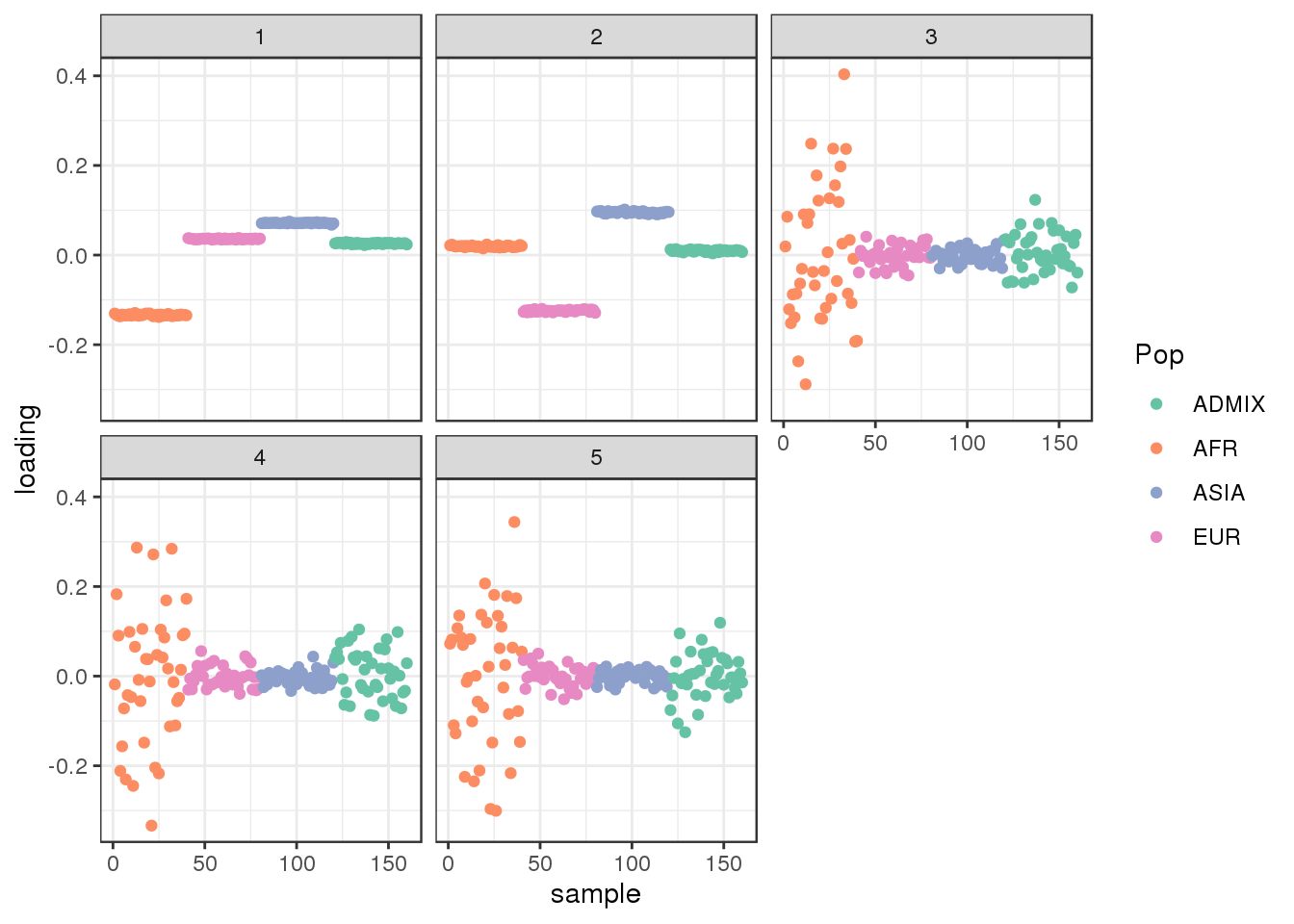

Version	Author	Date
407a5b0	Joseph Marcus	2020-05-13

Plot the first two factors against each other:

qplot(L_hat[,1], L_hat[,2], color=labs) + 
  xlab("PC1") + 
  ylab("PC2") + 
  scale_color_brewer(palette="Set2") + 
  theme_bw()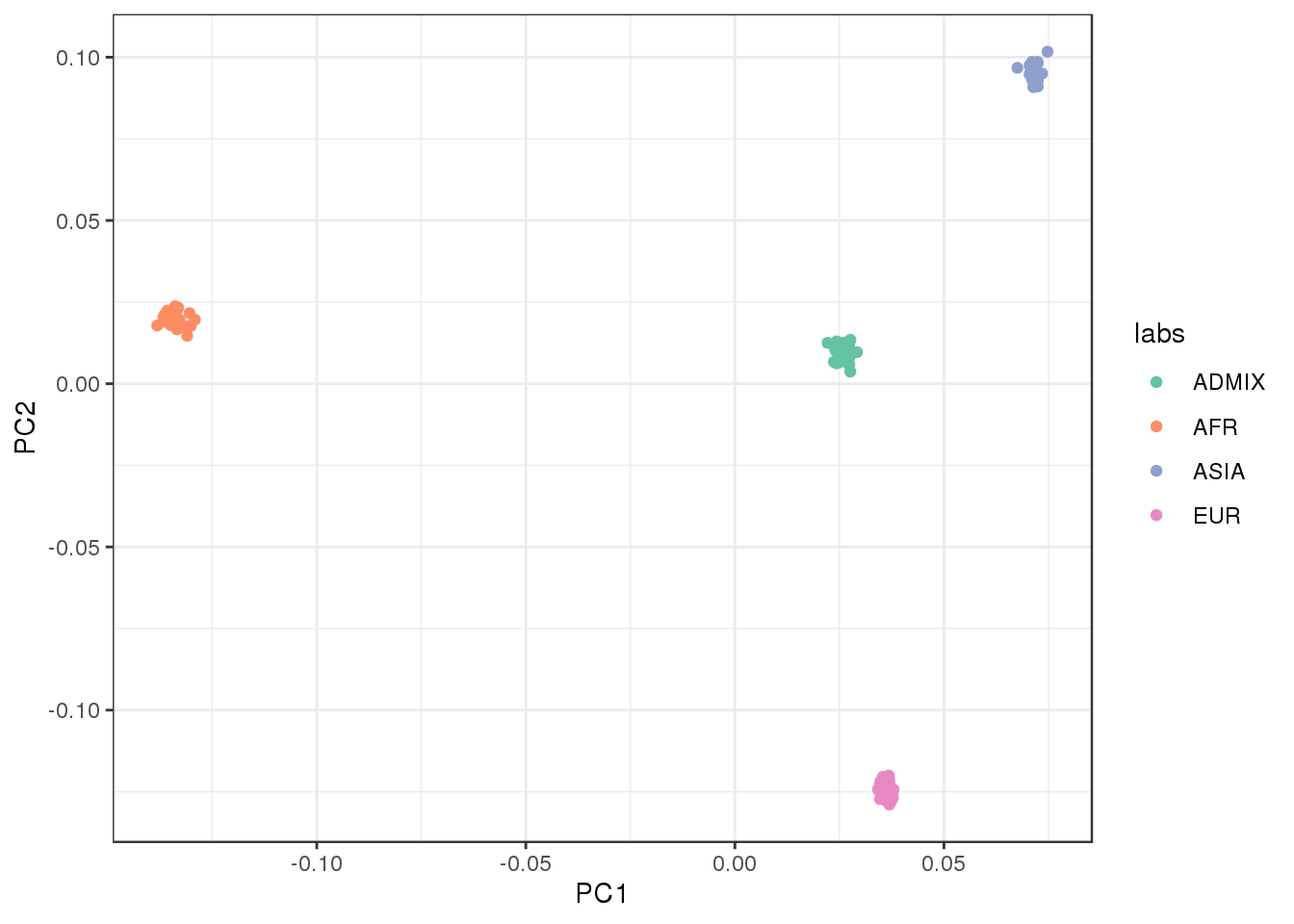

Version	Author	Date
407a5b0	Joseph Marcus	2020-05-13

the admixed population is in the center of the PC1 vs PC2 bi-plot.

ALStructure

Run ALStructure with \(K=3\):

admix_res <- alstructure::alstructure(t(Y), d_hat=3)
Qhat <- t(admix_res$Q_hat)
plot_loadings(Qhat, labs) + scale_color_brewer(palette="Set2")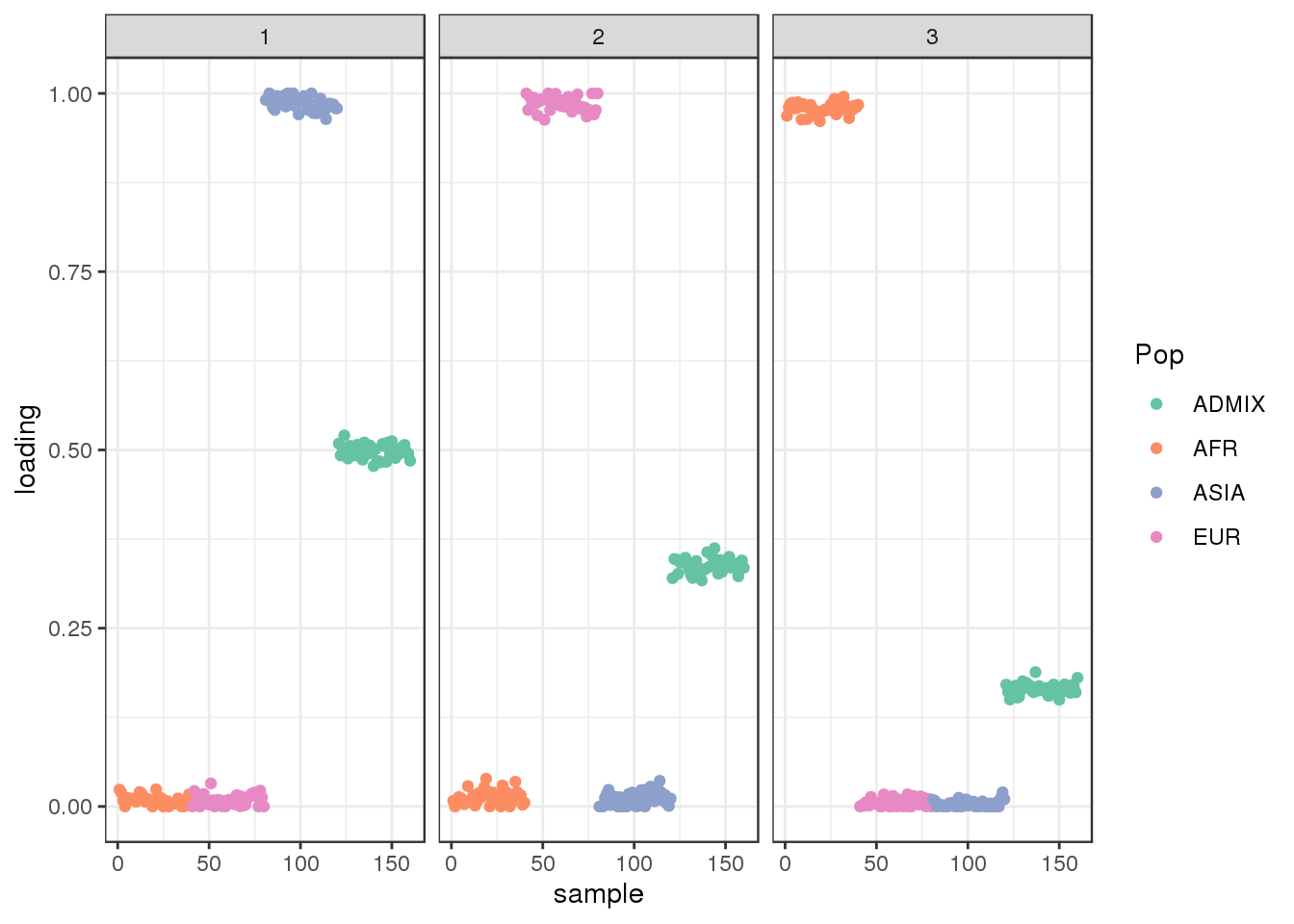

Version	Author	Date
407a5b0	Joseph Marcus	2020-05-13

view structure plot:

create_structure_plot(L=Qhat, labels=labs, colors=colors, ymax=1.01)

Scale for 'y' is already present. Adding another scale for 'y', which
will replace the existing scale.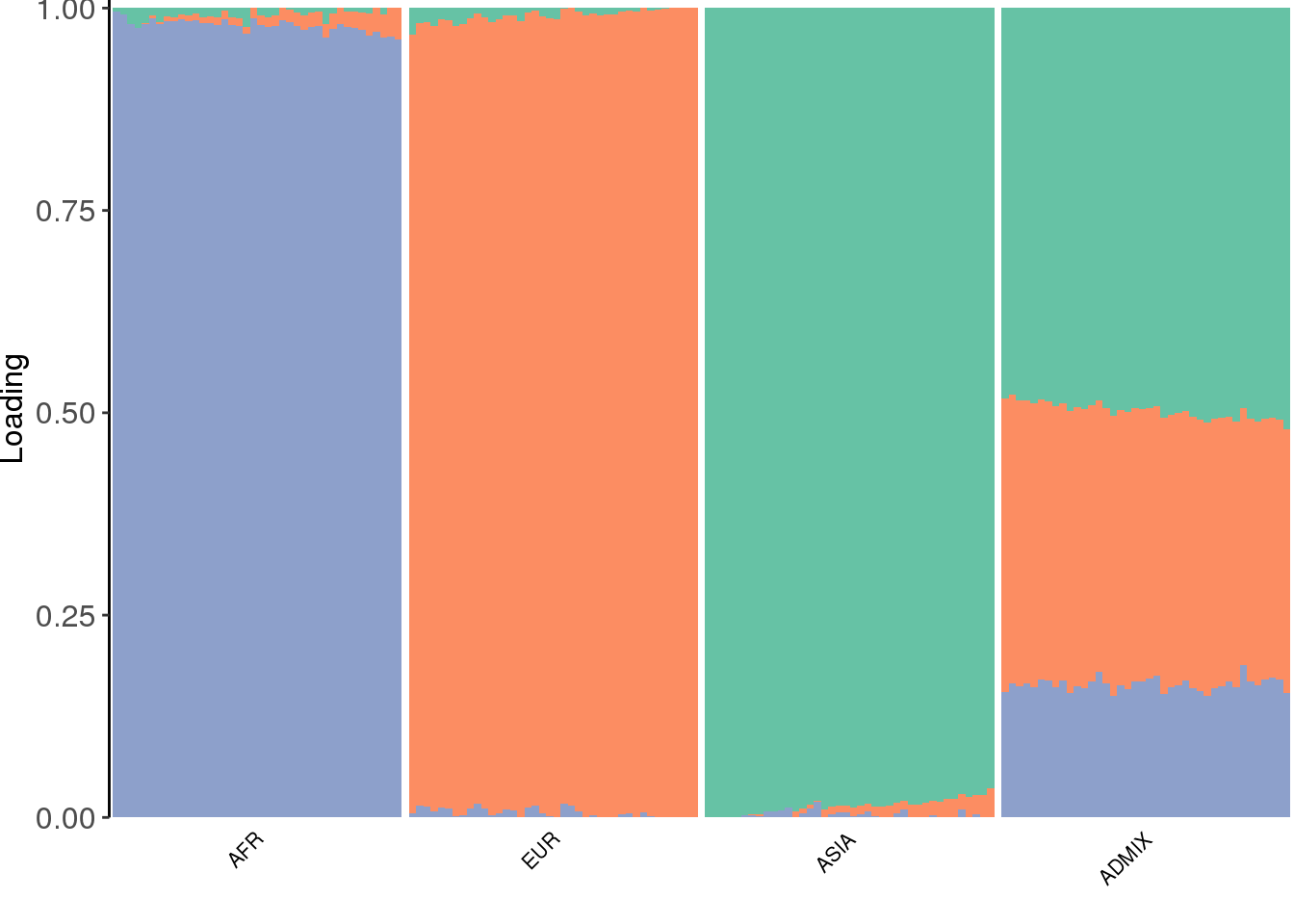

the three factors seems to represent “ancestral populations” from ASIA, EUR, and AFR and the admixed population draws ancestry from all three of them as expected.

flash [greedy]

Run the greedy algorithm:

fl <- flash(Y, 
            greedy.Kmax=8, 
            prior.family=c(prior.bimodal(), prior.normal()))

Adding factor 1 to flash object...
Adding factor 2 to flash object...
Adding factor 3 to flash object...
Adding factor 4 to flash object...
Adding factor 5 to flash object...
Factor doesn't significantly increase objective and won't be added.
Wrapping up...
Done.
Nullchecking 4 factors...
Done.

plot_loadings(fl$flash.fit$EF[[1]], labs) + scale_color_brewer(palette="Set2")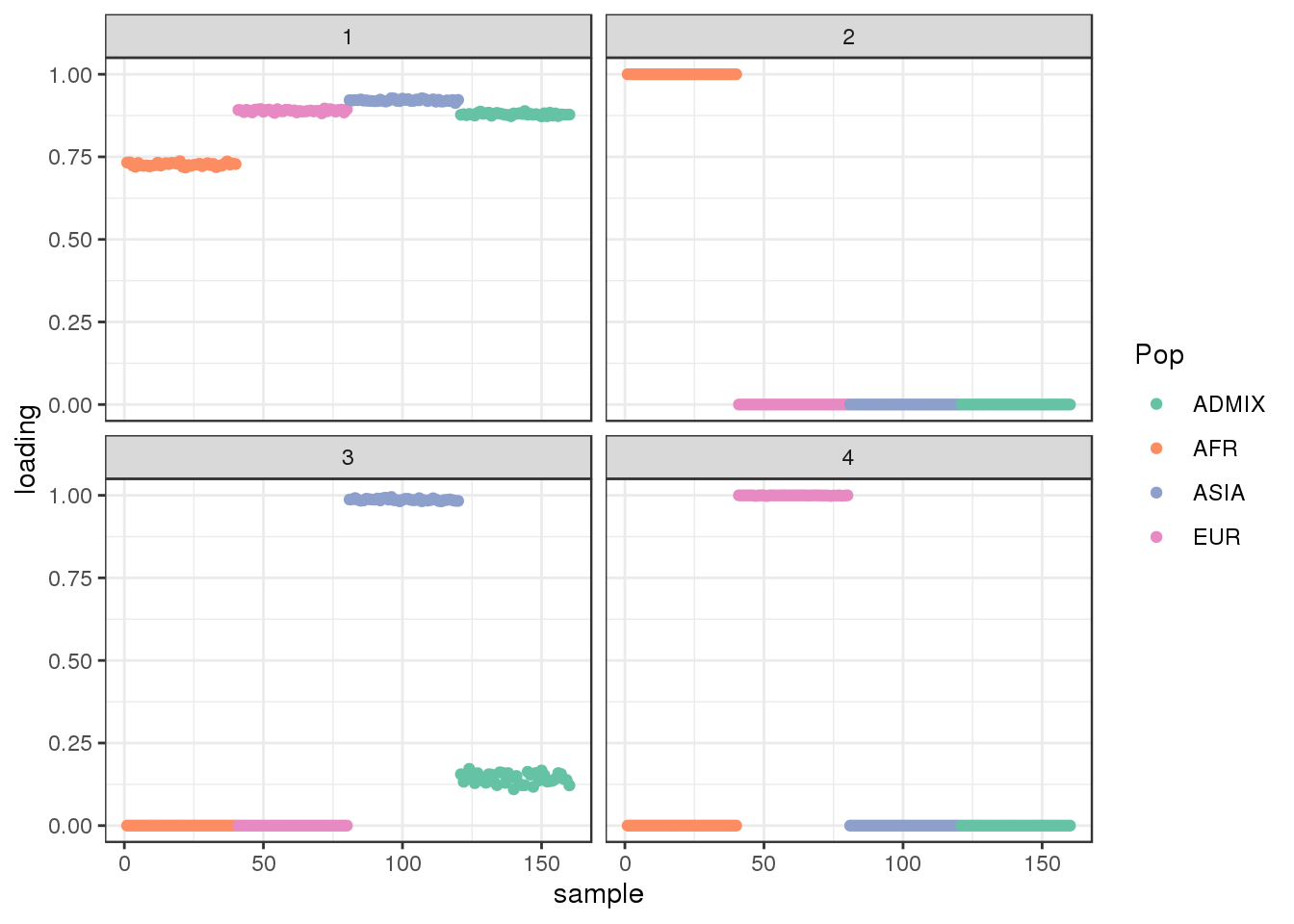

Version	Author	Date
407a5b0	Joseph Marcus	2020-05-13

view structure plot:

create_structure_plot(L=fl$flash.fit$EF[[1]], labels=labs, colors=colors)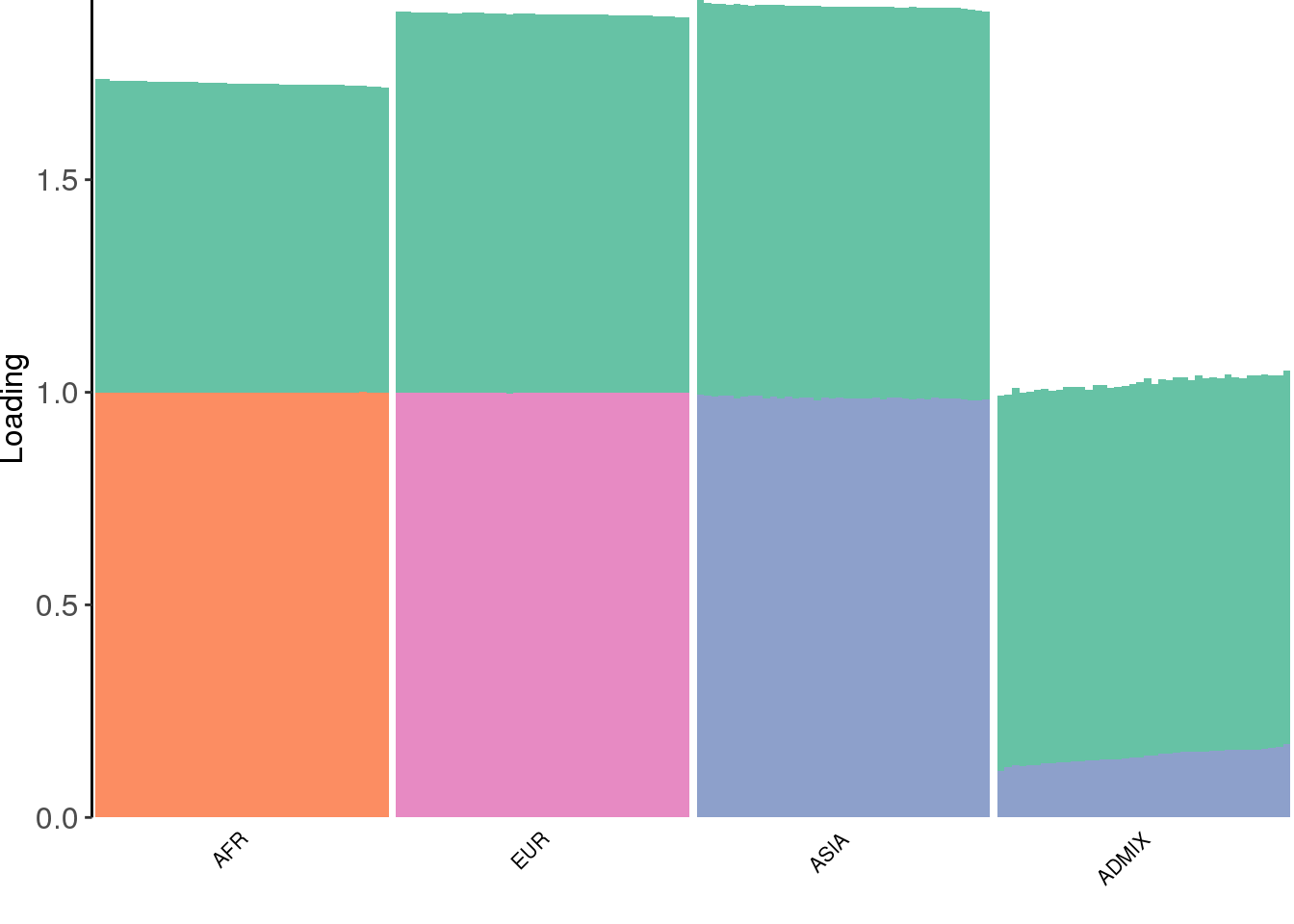

there are 4 factors learned by the greedy algorithm: one share factor with a slightly lower loading in the AFR population and 3 sparser factors. The third factor seems to be defined by ASIA individuals and the admixed population has a small weight on this factor.

flash [backfit]

Run flash [backfit] initializing from the greedy solution:

flbf <- fl %>% 
  flash.backfit() %>% 
  flash.nullcheck(remove=TRUE)

Backfitting 4 factors (tolerance: 5.88e-02)...
  Difference between iterations is within 1.0e+03...
  Difference between iterations is within 1.0e+02...
  Difference between iterations is within 1.0e+01...
  Difference between iterations is within 1.0e+00...
  Difference between iterations is within 1.0e-01...
Wrapping up...
Done.
Nullchecking 4 factors...
Done.

plot_loadings(flbf$flash.fit$EF[[1]], labs)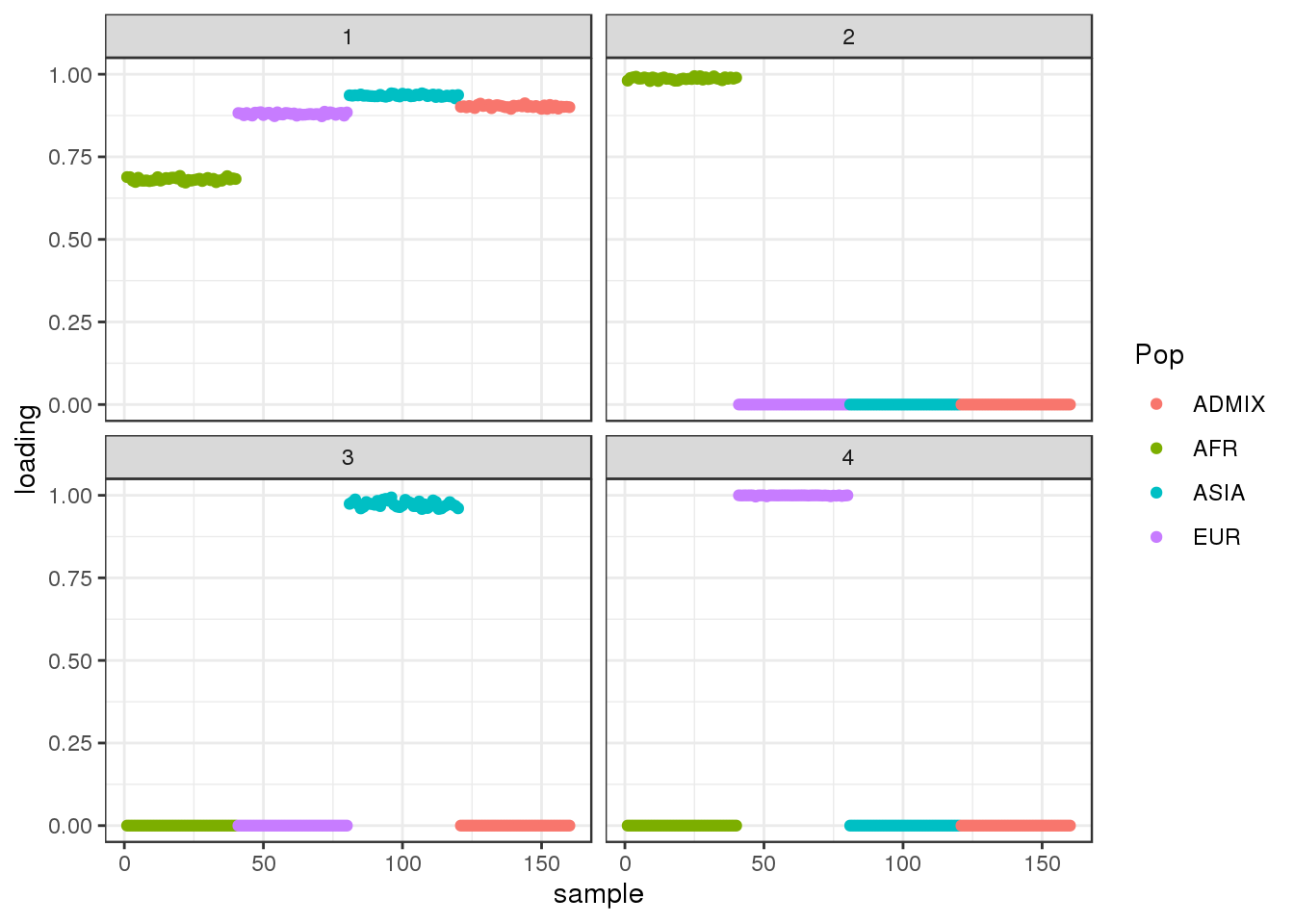

Version	Author	Date
407a5b0	Joseph Marcus	2020-05-13

view structure plot:

create_structure_plot(L=flbf$flash.fit$EF[[1]], labels=labs, colors=colors)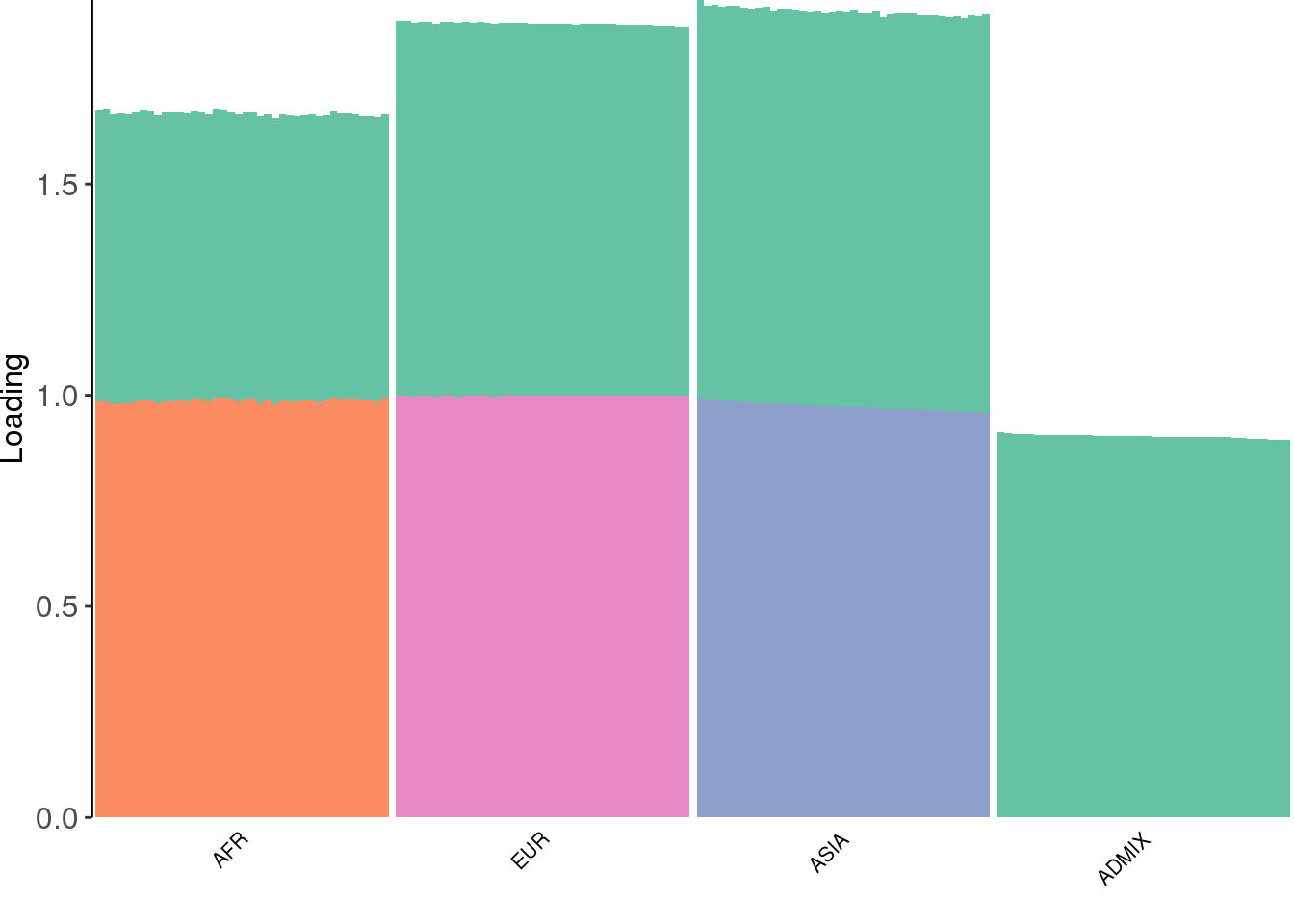

the results looks qualitatively similar to the greedy algorithm though now the the third factor is completely defined ASIA individuals.

drift

Run drift initializing from the greedy solution:

init <- init_from_flash(fl)
dr <- drift(init, miniter=2, maxiter=500, tol=0.01, verbose=TRUE)

   1 :    -3229696.286 
   2 :    -3228212.910 
   3 :    -3227165.987 
   4 :    -3226509.597 
   5 :    -3226125.724 
   6 :    -3225898.835 
   7 :    -3225767.675 
   8 :    -3225688.709 
   9 :    -3225636.374 
  10 :    -3225601.979 
  11 :    -3225577.336 
  12 :    -3225560.772 
  13 :    -3225549.245 
  14 :    -3225540.549 
  15 :    -3225533.633 
  16 :    -3225527.895 
  17 :    -3225522.022 
  18 :    -3225517.249 
  19 :    -3225513.311 
  20 :    -3225510.013 
  21 :    -3225507.188 
  22 :    -3225504.714 
  23 :    -3225502.511 
  24 :    -3225500.495 
  25 :    -3225498.561 
  26 :    -3225496.605 
  27 :    -3225494.601 
  28 :    -3225492.551 
  29 :    -3225490.591 
  30 :    -3225488.818 
  31 :    -3225487.163 
  32 :    -3225485.714 
  33 :    -3225484.471 
  34 :    -3225483.377 
  35 :    -3225482.388 
  36 :    -3225481.452 
  37 :    -3225480.461 
  38 :    -3225479.105 
  39 :    -3225477.126 
  40 :    -3225475.658 
  41 :    -3225474.857 
  42 :    -3225474.300 
  43 :    -3225473.842 
  44 :    -3225473.437 
  45 :    -3225473.071 
  46 :    -3225472.735 
  47 :    -3225472.425 
  48 :    -3225472.139 
  49 :    -3225471.872 
  50 :    -3225471.622 
  51 :    -3225471.389 
  52 :    -3225471.169 
  53 :    -3225470.962 
  54 :    -3225470.767 
  55 :    -3225470.582 
  56 :    -3225470.407 
  57 :    -3225470.241 
  58 :    -3225470.083 
  59 :    -3225469.933 
  60 :    -3225469.789 
  61 :    -3225469.652 
  62 :    -3225469.522 
  63 :    -3225469.397 
  64 :    -3225469.277 
  65 :    -3225469.163 
  66 :    -3225469.053 
  67 :    -3225468.948 
  68 :    -3225468.847 
  69 :    -3225468.750 
  70 :    -3225468.656 
  71 :    -3225468.567 
  72 :    -3225468.480 
  73 :    -3225468.397 
  74 :    -3225468.316 
  75 :    -3225468.239 
  76 :    -3225468.164 
  77 :    -3225468.091 
  78 :    -3225468.021 
  79 :    -3225467.953 
  80 :    -3225467.888 
  81 :    -3225467.824 
  82 :    -3225467.762 
  83 :    -3225467.702 
  84 :    -3225467.644 
  85 :    -3225467.587 
  86 :    -3225467.532 
  87 :    -3225467.478 
  88 :    -3225467.426 
  89 :    -3225467.375 
  90 :    -3225467.325 
  91 :    -3225467.277 
  92 :    -3225467.229 
  93 :    -3225467.183 
  94 :    -3225467.138 
  95 :    -3225467.093 
  96 :    -3225467.050 
  97 :    -3225467.007 
  98 :    -3225466.966 
  99 :    -3225466.925 
 100 :    -3225466.885 
 101 :    -3225466.846 
 102 :    -3225466.807 
 103 :    -3225466.769 
 104 :    -3225466.732 
 105 :    -3225466.696 
 106 :    -3225466.660 
 107 :    -3225466.624 
 108 :    -3225466.590 
 109 :    -3225466.556 
 110 :    -3225466.522 
 111 :    -3225466.489 
 112 :    -3225466.456 
 113 :    -3225466.424 
 114 :    -3225466.392 
 115 :    -3225466.361 
 116 :    -3225466.330 
 117 :    -3225466.300 
 118 :    -3225466.270 
 119 :    -3225466.241 
 120 :    -3225466.211 
 121 :    -3225466.183 
 122 :    -3225466.154 
 123 :    -3225466.126 
 124 :    -3225466.099 
 125 :    -3225466.071 
 126 :    -3225466.044 
 127 :    -3225466.018 
 128 :    -3225465.991 
 129 :    -3225465.965 
 130 :    -3225465.940 
 131 :    -3225465.914 
 132 :    -3225465.889 
 133 :    -3225465.864 
 134 :    -3225465.840 
 135 :    -3225465.816 
 136 :    -3225465.792 
 137 :    -3225465.768 
 138 :    -3225465.744 
 139 :    -3225465.721 
 140 :    -3225465.698 
 141 :    -3225465.675 
 142 :    -3225465.653 
 143 :    -3225465.631 
 144 :    -3225465.609 
 145 :    -3225465.587 
 146 :    -3225465.565 
 147 :    -3225465.544 
 148 :    -3225465.523 
 149 :    -3225465.502 
 150 :    -3225465.481 
 151 :    -3225465.460 
 152 :    -3225465.440 
 153 :    -3225465.420 
 154 :    -3225465.400 
 155 :    -3225465.380 
 156 :    -3225465.361 
 157 :    -3225465.341 
 158 :    -3225465.322 
 159 :    -3225465.303 
 160 :    -3225465.284 
 161 :    -3225465.266 
 162 :    -3225465.247 
 163 :    -3225465.229 
 164 :    -3225465.211 
 165 :    -3225465.193 
 166 :    -3225465.175 
 167 :    -3225465.157 
 168 :    -3225465.140 
 169 :    -3225465.122 
 170 :    -3225465.105 
 171 :    -3225465.088 
 172 :    -3225465.071 
 173 :    -3225465.054 
 174 :    -3225465.038 
 175 :    -3225465.021 
 176 :    -3225465.005 
 177 :    -3225464.989 
 178 :    -3225464.973 
 179 :    -3225464.957 
 180 :    -3225464.941 
 181 :    -3225464.925 
 182 :    -3225464.910 
 183 :    -3225464.894 
 184 :    -3225464.879 
 185 :    -3225464.863 
 186 :    -3225464.846 
 187 :    -3225464.829 
 188 :    -3225464.811 
 189 :    -3225464.792 
 190 :    -3225464.772 
 191 :    -3225464.752 
 192 :    -3225464.730 
 193 :    -3225464.708 
 194 :    -3225464.684 
 195 :    -3225464.660 
 196 :    -3225464.634 
 197 :    -3225464.607 
 198 :    -3225464.578 
 199 :    -3225464.548 
 200 :    -3225464.517 
 201 :    -3225464.483 
 202 :    -3225464.448 
 203 :    -3225464.411 
 204 :    -3225464.372 
 205 :    -3225464.330 
 206 :    -3225464.286 
 207 :    -3225464.239 
 208 :    -3225464.189 
 209 :    -3225464.136 
 210 :    -3225464.080 
 211 :    -3225464.020 
 212 :    -3225463.956 
 213 :    -3225463.887 
 214 :    -3225463.813 
 215 :    -3225463.734 
 216 :    -3225463.649 
 217 :    -3225463.557 
 218 :    -3225463.459 
 219 :    -3225463.352 
 220 :    -3225463.237 
 221 :    -3225463.111 
 222 :    -3225462.975 
 223 :    -3225462.828 
 224 :    -3225462.666 
 225 :    -3225462.490 
 226 :    -3225462.297 
 227 :    -3225462.086 
 228 :    -3225461.853 
 229 :    -3225461.598 
 230 :    -3225461.317 
 231 :    -3225461.007 
 232 :    -3225460.666 
 233 :    -3225460.290 
 234 :    -3225459.876 
 235 :    -3225459.422 
 236 :    -3225458.925 
 237 :    -3225458.385 
 238 :    -3225457.800 
 239 :    -3225457.170 
 240 :    -3225456.498 
 241 :    -3225455.822 
 242 :    -3225455.175 
 243 :    -3225454.557 
 244 :    -3225453.966 
 245 :    -3225453.402 
 246 :    -3225452.863 
 247 :    -3225452.349 
 248 :    -3225451.858 
 249 :    -3225451.390 
 250 :    -3225450.944 
 251 :    -3225450.520 
 252 :    -3225450.115 
 253 :    -3225449.731 
 254 :    -3225449.365 
 255 :    -3225449.018 
 256 :    -3225448.688 
 257 :    -3225448.374 
 258 :    -3225448.076 
 259 :    -3225447.793 
 260 :    -3225447.525 
 261 :    -3225447.270 
 262 :    -3225447.027 
 263 :    -3225446.797 
 264 :    -3225446.577 
 265 :    -3225446.369 
 266 :    -3225446.170 
 267 :    -3225445.981 
 268 :    -3225445.801 
 269 :    -3225445.629 
 270 :    -3225445.465 
 271 :    -3225445.308 
 272 :    -3225445.158 
 273 :    -3225445.015 
 274 :    -3225444.878 
 275 :    -3225444.746 
 276 :    -3225444.620 
 277 :    -3225444.499 
 278 :    -3225444.383 
 279 :    -3225444.272 
 280 :    -3225444.165 
 281 :    -3225444.062 
 282 :    -3225443.962 
 283 :    -3225443.867 
 284 :    -3225443.775 
 285 :    -3225443.686 
 286 :    -3225443.600 
 287 :    -3225443.518 
 288 :    -3225443.438 
 289 :    -3225443.361 
 290 :    -3225443.286 
 291 :    -3225443.214 
 292 :    -3225443.145 
 293 :    -3225443.077 
 294 :    -3225443.012 
 295 :    -3225442.948 
 296 :    -3225442.887 
 297 :    -3225442.827 
 298 :    -3225442.769 
 299 :    -3225442.713 
 300 :    -3225442.659 
 301 :    -3225442.606 
 302 :    -3225442.554 
 303 :    -3225442.504 
 304 :    -3225442.456 
 305 :    -3225442.408 
 306 :    -3225442.362 
 307 :    -3225442.317 
 308 :    -3225442.274 
 309 :    -3225442.231 
 310 :    -3225442.190 
 311 :    -3225442.150 
 312 :    -3225442.110 
 313 :    -3225442.072 
 314 :    -3225442.035 
 315 :    -3225441.998 
 316 :    -3225441.962 
 317 :    -3225441.928 
 318 :    -3225441.894 
 319 :    -3225441.861 
 320 :    -3225441.828 
 321 :    -3225441.796 
 322 :    -3225441.766 
 323 :    -3225441.735 
 324 :    -3225441.706 
 325 :    -3225441.677 
 326 :    -3225441.648 
 327 :    -3225441.621 
 328 :    -3225441.593 
 329 :    -3225441.567 
 330 :    -3225441.541 
 331 :    -3225441.515 
 332 :    -3225441.490 
 333 :    -3225441.466 
 334 :    -3225441.442 
 335 :    -3225441.418 
 336 :    -3225441.395 
 337 :    -3225441.373 
 338 :    -3225441.350 
 339 :    -3225441.329 
 340 :    -3225441.307 
 341 :    -3225441.286 
 342 :    -3225441.266 
 343 :    -3225441.246 
 344 :    -3225441.226 
 345 :    -3225441.206 
 346 :    -3225441.187 
 347 :    -3225441.168 
 348 :    -3225441.150 
 349 :    -3225441.131 
 350 :    -3225441.114 
 351 :    -3225441.096 
 352 :    -3225441.079 
 353 :    -3225441.062 
 354 :    -3225441.045 
 355 :    -3225441.028 
 356 :    -3225441.012 
 357 :    -3225440.996 
 358 :    -3225440.981 
 359 :    -3225440.965 
 360 :    -3225440.950 
 361 :    -3225440.935 
 362 :    -3225440.920 
 363 :    -3225440.906 
 364 :    -3225440.891 
 365 :    -3225440.877 
 366 :    -3225440.863 
 367 :    -3225440.849 
 368 :    -3225440.836 
 369 :    -3225440.823 
 370 :    -3225440.809 
 371 :    -3225440.796 
 372 :    -3225440.784 
 373 :    -3225440.771 
 374 :    -3225440.759 
 375 :    -3225440.746 
 376 :    -3225440.734 
 377 :    -3225440.722 
 378 :    -3225440.710 
 379 :    -3225440.699 
 380 :    -3225440.687 
 381 :    -3225440.676 
 382 :    -3225440.665 
 383 :    -3225440.653 
 384 :    -3225440.642 
 385 :    -3225440.632 
 386 :    -3225440.621 
 387 :    -3225440.610 
 388 :    -3225440.600 
 389 :    -3225440.590 
 390 :    -3225440.579 
 391 :    -3225440.569 
 392 :    -3225440.559

plot_loadings(dr$EL, labs)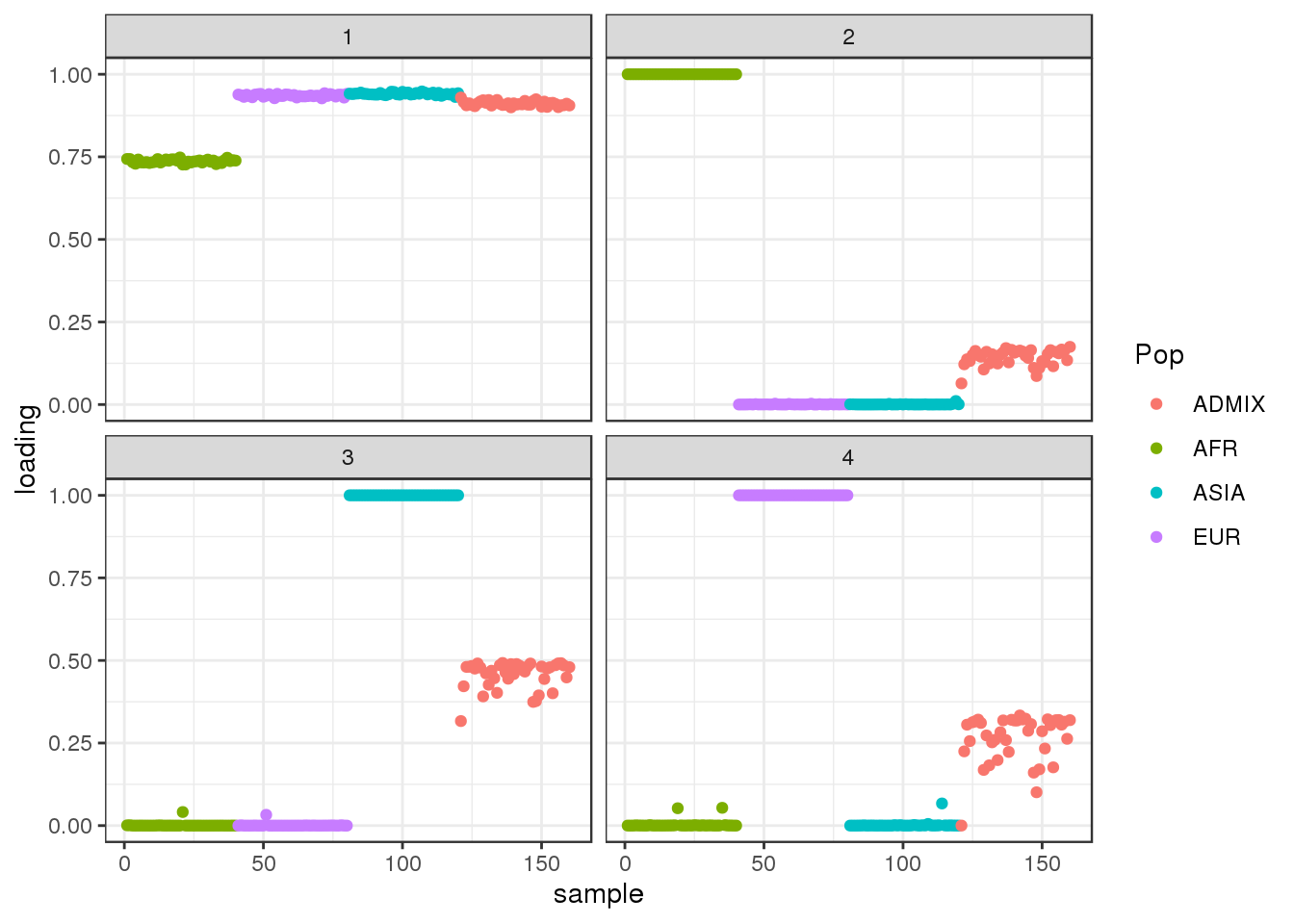

Version	Author	Date
407a5b0	Joseph Marcus	2020-05-13

view structure plot:

create_structure_plot(L=dr$EL, labels=labs, colors=colors)

the drift algorithm seems to give a pretty different result from flash. There is one shared factor but then the admixed population has intermediate values on all the other factors. Here are the admixture proportions from the coalescent simulation:

ADMIX percentage 1/6 | Amount African admixture
ADMIX percentage 1/3 | Amount European admixture
ADMIX percentage 1/2 | Amount Asian admixture

which actually qualitatively lines up with ADMIX population loadings on factors 2-4! It’s kinda interesting that we recapitulate a similar behavior we saw in real data for “known” admixed populations when we applied flash and drift to Human Origins data.

sessionInfo()

R version 3.5.1 (2018-07-02)
Platform: x86_64-pc-linux-gnu (64-bit)
Running under: Scientific Linux 7.4 (Nitrogen)

Matrix products: default
BLAS/LAPACK: /software/openblas-0.2.19-el7-x86_64/lib/libopenblas_haswellp-r0.2.19.so

locale:
 [1] LC_CTYPE=en_US.UTF-8       LC_NUMERIC=C              
 [3] LC_TIME=en_US.UTF-8        LC_COLLATE=en_US.UTF-8    
 [5] LC_MONETARY=en_US.UTF-8    LC_MESSAGES=en_US.UTF-8   
 [7] LC_PAPER=en_US.UTF-8       LC_NAME=C                 
 [9] LC_ADDRESS=C               LC_TELEPHONE=C            
[11] LC_MEASUREMENT=en_US.UTF-8 LC_IDENTIFICATION=C       

attached base packages:
[1] stats     graphics  grDevices utils     datasets  methods   base     

other attached packages:
 [1] alstructure_0.1.0  RColorBrewer_1.1-2 forcats_0.5.0     
 [4] stringr_1.4.0      dplyr_0.8.5        purrr_0.3.4       
 [7] readr_1.3.1        tidyr_1.0.2        tibble_3.0.1      
[10] tidyverse_1.3.0    reshape2_1.4.3     ggplot2_3.3.0     
[13] drift.alpha_0.0.9  flashier_0.2.4     lfa_1.9.0         

loaded via a namespace (and not attached):
 [1] httr_1.4.1       jsonlite_1.6     modelr_0.1.6     assertthat_0.2.1
 [5] mixsqp_0.3-17    cellranger_1.1.0 yaml_2.2.0       ebnm_0.1-24     
 [9] pillar_1.4.3     backports_1.1.6  lattice_0.20-38  glue_1.4.0      
[13] digest_0.6.25    promises_1.0.1   rvest_0.3.5      colorspace_1.4-1
[17] htmltools_0.3.6  httpuv_1.4.5     Matrix_1.2-15    plyr_1.8.4      
[21] pkgconfig_2.0.3  invgamma_1.1     broom_0.5.6      haven_2.2.0     
[25] corpcor_1.6.9    scales_1.1.0     whisker_0.3-2    later_0.7.5     
[29] git2r_0.26.1     farver_2.0.3     generics_0.0.2   ellipsis_0.3.0  
[33] withr_2.2.0      ashr_2.2-50      cli_2.0.2        magrittr_1.5    
[37] crayon_1.3.4     readxl_1.3.1     evaluate_0.14    fs_1.3.1        
[41] fansi_0.4.1      nlme_3.1-137     xml2_1.3.2       truncnorm_1.0-8 
[45] tools_3.5.1      hms_0.5.3        lifecycle_0.2.0  munsell_0.5.0   
[49] reprex_0.3.0     irlba_2.3.3      compiler_3.5.1   rlang_0.4.5     
[53] grid_3.5.1       rstudioapi_0.11  labeling_0.3     rmarkdown_1.10  
[57] gtable_0.3.0     DBI_1.0.0        R6_2.4.1         lubridate_1.7.4 
[61] knitr_1.20       workflowr_1.6.1  rprojroot_1.3-2  stringi_1.4.6   
[65] parallel_3.5.1   SQUAREM_2020.2   Rcpp_1.0.4.6     vctrs_0.2.4     
[69] dbplyr_1.4.3     tidyselect_1.0.0

AmericanAdmixture_4B11

Joseph Marcus

2020-05-13

Imports

Data

PCA

ALStructure

flash [greedy]

flash [backfit]

drift